STOCHASTIQUES (PROCESSUS)

STOCHASTIQUES (PROCESSUS)

Le calcul des probabilités classique ^{[cf. PROBABILITÉS (CALCUL DES)]} s’applique à des épreuves où chaque résultat possible (ou éventualité) est un nombre . Or il existe beaucoup de situations réelles relevant de modèles aléatoires, mais d’une nature plus complexe. Considérons, par exemple, l’évolution d’une rivière: en raison du caractère périodique du phénomène, on peut l’étudier au cours d’une année, et, dans ce cas, une épreuve consiste à observer les débits au cours d’une année entière. Un événement élémentaire (une éventualité) est alors une fonction t 料 x qui, au temps t , compté en année et variant de 0 à 1, associe le débit x (t ) à la date t .

Comme autres exemples citons: le développement d’une population (évolution de l’effectif de la population en fonction du temps); la propagation d’une épidémie; l’évolution de la demande d’un bien par une clientèle; la variation du nombre de clients présents à un poste de service, etc. Ainsi, en physique, en biologie, dans les sciences humaines et même en musique, on est conduit fréquemment à s’intéresser à des évolutions d’une grandeur au cours du temps où le «hasard» intervient à chaque instant. La réalisation de l’épreuve est une fonction du temps. Le modèle mathématique est une fonction aléatoire, mais dont l’argument est le temps , d’où la définition donnée au chapitre 1. L’étude des épreuves répétées en calcul des probabilités avait conduit P. S. Laplace, J. Bernoulli et A. de Moivre à considérer des suites aléatoires additives et stationnaires, c’est-à-dire telles que les différences (X^{n +1} 漣 Xⁿ ) soient mutuellement indépendantes et parentes. Seuls S. D. Poisson et P. L. Tchebychev s’étaient intéressés à des suites non stationnaires. Suivant une autre voie, F. Galton et H. W. Watson, en étudiant l’extinction des familles, introduisent, en 1874, les processus dits de ramifications (où X^{n +1} est la somme de Xⁿ variables aléatoires entières indépendantes et parentes); puis A. A. Markov étudie, de 1907 à 1912, des «cas remarquables d’épreuves dépendantes».

Ainsi, au XX^e siècle, la théorie s’est progressivement édifiée à propos de problèmes très variés, allant de la physique théorique à l’organisation des entreprises. Les premières bases théoriques ont été posées par A. N. Kolmogorov en 1931; J. L. Doob a publié, en 1953, un traité fondamental sur l’ensemble de la question: Stochastic Processes .

1. Définition générale

On appelle processus stochastique ou processus aléatoire toute famille de variables aléatoires X^t . Cela signifie qu’à tout t 捻 T est associée une variable aléatoire prenant ses valeurs dans un ensemble numérique 劉. On note le processus X^t . Si T est dénombrable, on dit que le processus est discret ; si T est un intervalle, on dit que le processus est permanent .

La définition effective d’un processus stochastique soulève de sérieuses difficultés tant théoriques que pratiques. On pourrait définir un processus en se référant au schéma général de Kolmogorov (cf. PROBABILITÉS, chap. 2) et considérer un ensemble 行 de fonctions possibles, puis une tribu 龍 de parties de 行, et enfin définir une probabilité (fonction positive et 靖-additive d’ensembles) sur 龍. Ce point de vue très abstrait (cf. J. L. Doob, Stochastic Processes , chap. II) se prête mal aux applications, car on ne peut effectivement probabiliser que des ensembles numériques (ou ceux qui leur sont isomorphes). Une définition constructive est la seule qui se prête aux applications. Ajoutons que, si un processus stochastique est une fonction aléatoire, son argument est le temps, au déroulement irréversible et inéluctable, ce qui influe fortement sur la nature des problèmes pratiques posés: essentiellement la prédiction (ou extrapolation), c’est-à-dire le comportement de X^t pour t 礪 t ⁰ connaissant les valeurs prises par X^t pour t 諒 t ⁰.

On dit qu’on a défini la loi temporelle d’un processus si, pour toute valeur de l’entier n et pour toute valeur des instants t ¹, t ², ..., tⁿ , on connaît la loi jointe de l’ensemble aléatoire:

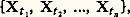par exemple par la donnée de la fonction de répartition (cf. calcul des PROBABILITÉS, chap. 3) de cet ensemble:

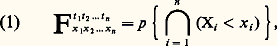où p est la probabilité.

Cette définition appelle les remarques suivantes:

a ) L’ensemble dénombrable de fonctions de répartition (1) doit être cohérent, c’est-à-dire que chaque fonction F doit être une fonction symétrique des couples (tⁱ , xⁱ ). De plus, la donnée de la loi d’un ensemble:

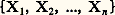définit la loi de tout sous-ensemble, et on doit avoir, pour tout n , l’égalité:

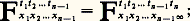Kolmogorov a montré, en 1933, que, s’il en est ainsi, une tribu probabilisée de fonctions est bien définie par (1) et qu’elle obéit à ces relations.

b ) La loi temporelle est dite définition faible du processus, car les événements probabilisés à partir de la loi temporelle sont uniquement ceux qui s’expriment par un ensemble dénombrable d’inégalités telles que X^ti 麗 aⁱ ou X^tj 礪 b^j . Toutefois, des extensions du domaine probabilisé sont possibles en admettant que x (t ) appartienne presque sûrement à une classe particulière de fonctions (cf. J. L. Doob, Stochastic Processes ; R. Fortet et A. Blanc-Lapierre, Théorie des fonctions aléatoires ).

c ) L’estimation de la loi temporelle d’un processus observé est un problème pratique impossible à résoudre. Les phénomènes évolutifs étudiés ne peuvent généralement pas être provoqués; aussi le chercheur ne dispose-t-il le plus souvent que d’un très petit nombre de réalisations du processus. Dans ces conditions, il n’est pas possible d’estimer des fonctions de répartition, même si on limite à quelques unités le nombre des paramètres (ensemble tⁱ théoriquement dénombrable). Il est donc indispensable d’étudier des classes particulières de processus ou, mieux encore, des familles de processus dépendant d’un nombre restreint de paramètres. Les principales classes sont: les processus de Markov et les processus de renouvellement; les processus à accroissements aléatoires indépendants ; enfin, les processus laplaciens et les processus du second ordre.

2. Processus ponctuels

Un processus ponctuel concerne les instants où se réalisent des événements instantanés d’une classe particulière: par exemple, les débuts de pannes d’un ensemble de machines, les instants d’arrivée d’un mobile à un système de contrôle, les instants de naissance d’une particule ou d’un individu d’une population. Une réalisation d’un tel processus est décrite par la donnée d’une suite croissante d’instants t ¹, t ² ..., (ceux où se réalise le phénomène) ou par une suite de points P¹, P²,... sur l’échelle des temps, avec OPⁿ = tⁿ , d’où la dénomination de processus ponctuel .

On peut associer à un tel processus un processus numérique X^t , où X représente le nombre d’événements obtenus sur [0, t ]. La fonction aléatoire X^t est un cas particulier de processus numérique: elle croît par sauts de une unité en des instants aléatoires (discontinuités mobiles). Toutefois, l’origine particulière de ce type de processus conduit à le définir de manière mieux adaptée aux besoins.

Définition par nombres d’événements sur un ensemble d’intervalles disjoints . Soit k intervalles disjoints ]tⁱ , tⁱ ], avec i = 1, 2, ..., k , et soit Nⁱ le nombre d’événements obtenus sur ]tⁱ , tⁱ ], c’est-à-dire Nⁱ = X^ti size=1 漣 X^ti size=1. On donne, pour tout k et pour tout ensembletⁱ , tⁱⁱ , la loi jointe de¹, ², ..., N^k.

Définition par intervalles successifs . Posons U¹ = t ¹ et Uⁿ = tⁿ 漣 t^{n -1} = P^{n -1}Pⁿ . On donne la suite des lois conditionnelles des Uⁿ connaissant U¹, U², ..., U^{n -1} pour tout n entier positif.

Il convient, à propos des processus ponctuels, de reprendre les remarques sur le caractère trop général de ce modèle. En vue des applications, on doit tout d’abord considérer une famille convenable de processus ponctuels, puis estimer le ou les paramètres du modèle retenu pour le ou les appliquer à un exemple particulier.

Le processus ponctuel de Poisson est le cas le plus simple et le plus important. On l’obtient en posant les axiomes suivants.

Axiome d’indépendance : Pour tout k , quels que soient t ¹, t ¹ , ..., t ^k , t^k , les variables aléatoires ¹, ², ..., N^k sont indépendantes dans leur ensemble.

Axiome d’uniformité : La loi du nombre d’événements obtenus sur ]t , t + h ] est indépendante de t . On suppose, de plus, que la probabilité d’obtenir plusieurs événements au même instant est nulle et, enfin, que la probabilité p (h ) de n’obtenir aucun événement sur ]t , t + h ] est strictement positive et strictement inférieure à 1 pour tout h 礪 0.

Dans ces conditions, les nombres Nⁱ (indépendants) obéissent à des lois de Poisson : le paramètre est c (tⁱ 漣 tⁱ ) pour Nⁱ ; de plus, les intervalles successifsUⁱⁱ sont indépendants en probabilité et obéissent tous à la même loi dite 塚¹, ou exponentielle, d’expression élémentaire:

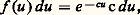où c est la densité du processus.

Ce modèle peut être obtenu à partir d’un processus ponctuel discret. Supposons qu’un événement puisse se produire en chacun des instants 0,1/n , 2/n , ..., éléments de l’ensemble N(1/n ), avec la même probabilité p = c /n , et que les résultats (réalisation ou non de l’événement à un instant) soient indépendants en probabilité. On obtient un processus ponctuel discret qui obéit aux axiomes précédents, mais avec ici t 捻 N(1/n ). Si n tend vers l’infini, on obtient à la limite un processus ponctuel permanent: c’est le processus de Poisson de densité c .

En raison de l’axiome d’indépendance, le processus de Poisson a des propriétés très simples fort appréciées des utilisateurs. Ce modèle représente remarquablement la radioactivité naturelle (suite des enregistrements d’un compteur de Geiger-Müller) et certains phénomènes analogues d’émissions radioactives. Il représente assez bien les occurrences de pannes de systèmes électriques ou électroniques complexes; en revanche, son utilisation pour représenter des arrivées de bateaux, d’avions, de clients, etc. ne doit pas se faire sans examen critique préalable. Les hypothèses qui justifient l’emploi du modèle sont clairement décrites à partir du modèle discret: il y a un très grand nombre d’événements possibles, les réalisations sont indépendantes les unes des autres et le phénomène conserve la même intensité au cours du temps.

3. Processus à accroissements aléatoires indépendants

Soit X^t un processus numérique et t ¹, t ², ..., t^k une suite croissante d’instants. Soit:

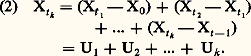Le processus est dit à accroissements aléatoires indépendants si, pour tout k et tous t ¹, t ², ..., t^k , les variables aléatoires:

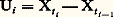sont indépendantes en probabilité. La marche au hasard sur une droite fut le premier exemple étudié de ce type de processus.

Marche au hasard

Un mobile se déplace sur un axe Ox par pas d’une unité chaque fois dans l’un ou l’autre sens avec des probabilités égales. S’il fait un pas par unité de temps en partant de 0 à l’instant t = 0, il est à l’instant n en un point Pⁿ tel que:

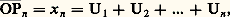où les Uⁱ sont des variables aléatoires indépendantes et parentes, chacune prenant les valeurs + 1 ou 漣 1 avec des probabilités égales. Le processus X^t , défini pour t 捻 N, est à accroissements indépendants.

Ce modèle se généralise, d’une part, par la promenade au hasard sur un réseau d’un espace euclidien à n dimensions; à chaque étape, le mobile se déplace de une unité dans l’un des 2 n sens possibles avec des probabilités égales (cf. calcul des PROBABILITÉS, chap. 11). Il se généralise, d’autre part, en supposant que les accroissements indépendants et parents Uⁱ obéissent à une loi quelconque.

Le processus Xⁿ obtenu peut représenter la fortune d’un joueur qui renouvelle des paris successifs. La fonction Uⁱ est alors le gain net et aléatoire d’un coup. Le processus Xⁿ peut aussi représenter l’évolution de la situation financière d’une compagnie d’assurance.

Toute fonction X^t obtenue ici varie par sauts d’amplitude aléatoire, mais en des instants déterminés et connus d’avance t = 1, 2, ..., n , ...

On obtient des modèles beaucoup plus originaux en supposant que X^t varie soit d’une manière continue, soit par sauts en des instants aléatoires. Deux cas particuliers très importants illustrent ces deux généralisations: le processus de Poisson et celui de Wiener-Lévy.

Fonction indicatrice d’un processus de Poisson

Soit X^t le nombre de points obtenus sur [0, t ] dans un processus ponctuel de Poisson de densité c . La fonction X^t croît par sauts de une unité en des points aléatoires (processus ponctuel de Poisson); c’est un processus à accroissements indépendants, et l’accroissement Uⁱ sur l’intervalle [t , tⁱ ] obéit à la loi de Poisson de paramètre c (tⁱ 漣 t^{i -1}). On obtient un modèle plus général en supposant que, sur tout intervalle ]t , t ], l’accroissement de X^t obéit à une loi de Poisson dont le paramètre est une fonction g (t , t ). Ici g est une fonction positive et additive d’intervalles: c’est une mesure; elle est définie par sa fonction de distribution:

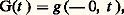et l’on a:

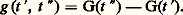Le processus ponctuel des points de discontinuité de X^t est dit processus de Poisson non uniforme.

Processus de Wiener-Lévy ou fonction du mouvement brownien linéaire

Supposons qu’une particule puisse se déplacer sur un axe 0x . À chaque instant, elle reçoit une légère impulsion dans l’un ou l’autre sens avec des probabilités égales. Pour atteindre un schéma continu, on doit procéder par passage à la limite d’une suite de processus discrets. Entre les dates t et t + 1/n , la particule subit un déplacement aléatoire qui prend la valeur 1/ 連n avec la probabilité 1/2 et 漣 1/ 連n avec la probabilité 1/2. La fonction caractéristique de cet accroissement est cos t / 連n , et, par suite, pendant la durée h , la somme des accroissements (indépendants) a pour fonction caractéristique (cos t / 連n )^hn . Si le nombre n tend vers l’infini, la loi limite de l’accroissement a pour fonction caractéristique exp (face=F0019 漣 t ²h /2): c’est la loi de Laplace-Gauss centrée de variance h. Tel est le processus de Wiener-Lévy dont on peut donner la définition suivante: X^t , défini sur t 閭 0, est à accroissements indépendants, et, sur tout intervalle ]t , t ], l’accroissement de la fonction X obéit à la loi de Laplace-Gauss centrée de variance (t 漣 t ). La fonction X^t est presque sûrement continue; pourtant, il n’est pas possible de tracer le graphe d’une réalisation du processus, car la fonction est presque sûrement sans dérivée et à variation non bornée sur tout intervalle fini. Ce schéma imaginé par Bachelier (1900) a été étudié plus complètement par N. Wiener (1923), puis par Paul Lévy (1937-1948).

Cas laplacien

Soit G(t ) une fonction monotone croissante sur t 礪 0 et X^t un processus à accroissements indépendants réalisant X⁰ = 0. On suppose que, sur tout intervalle ]t , t ], l’accroissement de X^t obéit la loi de Laplace-Gauss centrée de variance G(t ) 漣 G(t ), donc que X^t obéit à la loi de Laplace-Gauss centrée de variance G(t ). On s’assure facilement que ces conditions sont compatibles. La fonction G(t ) est dite fonction de distribution des variances. Le processus de Wiener-Lévy correspond au cas où G(t ) = t , processus uniforme de densité 1.

Théorie générale

La théorie générale des processus à accroissements indépendants a été faite par Paul Lévy en 1937. Elle est en relation étroite avec l’arithmétique des lois de probabilité (cf. calcul des PROBABILITÉS, chap. 5), comme le montre la relation (2) qui se traduit de la manière suivante en termes de fonctions caractéristiques: Si 切^{(t )}(z ) est la seconde fonction caractéristique de X^t , à savoir:

E étant l’espérance mathématique, et 切^{(h )}(z ) la seconde fonction caractéristique de l’accroissement U^h de X sur (t^{h -1}, t^h ), alors on a: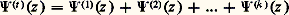

pour toute partition de (0, t^k ).

De plus, si X¹(t ) et X²(t ) sont deux processus indépendants à accroissements indépendants, et, si a ¹ et a ² sont deux constantes arbitraires, alors:

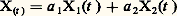est aussi un processus à accroissements indépendants. Ces deux remarques sont à la base de la théorie. Le processus le plus général s’obtient par opération linéaire à partir des cas particuliers suivants:

Le processus X^t présente des discontinuités fixes (en des instants déterminés);

Le processus X^t présente des discontinuités mobiles: les sauts d’amplitude u se font en des instants obéissant à un processus de Poisson non uniforme;

Le processus X^t est un processus laplacien à accroissements indépendants.

On voit que les lois de Poisson et de Laplace-Gauss jouent un rôle fondamental dans une théorie qui met clairement en évidence leurs propriétés. Il convient de mentionner deux autres cas particuliers de processus à accroissements indépendants: X^t obéit à la loi de Cauchy de paramètre t , soit:

et X^t obéit à la loi gamma de paramètre t , soit: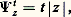

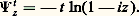4. Processus de Markov

L’étude statistique de la succession des caractères utilisés pour composer un texte dans une langue particulière a suggéré à Markov un schéma d’enchaînement aléatoire avec liaison (par exemple, en anglais, la fréquence de la lettre h après un t est très supérieure à ce qu’elle est après un d ).

Soit X^t , soit t ¹, t ², ..., tⁿ , t une suite croissante d’instants, soit enfin X¹, X², ..., Xⁿ , X les valeurs aléatoires correspondantes, la loi conditionnelle de X connaissant (X¹, X², ..., Xⁿ ) dépend de (tⁿ , Xⁿ , t ), c’est-à-dire que les valeurs successives sont liées entre elles; Markov fait l’hypothèse que la dernière valeur connue et le dernier instant résument toute l’information; on développe plus complètement la théorie en supposant que les lois conditionnelles sont invariantes par translation sur l’échelle des temps, c’est-à-dire que:

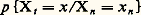ne dépend que de (t 漣 tⁿ ) et de xⁿ ; le processus de Markov est alors dit homogène dans le temps . Deux cas sont à considérer relativement à l’ensemble T des instants: T est dénombrable (processus discret ou suite de Markov); T est continu (processus permanent). De plus, trois cas sont à distinguer relativement à l’ensemble 劉 des valeurs possibles de X (états du système): cas fini 劉 =1, 2, ..., k; cas dénombrable 劉 = N; cas continu 劉 = R.

Cas fini

Considérons le cas où 劉 =1, 2, ..., k et T =t ¹, t ², ..., tⁿ , .... Il suffit de donner la loi initiale des états, c’est-à-dire le vecteur colonne P ⁰ de composantes p ^0h = pX⁰ = h, pour h = 1, 2, ..., k , et la matrice carrée, d’ordre k , M = 瑩p^ij 瑩, où:

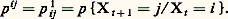La matrice M est dite matrice de Markov ou matrice des probabilités de passage . La loi des états à la date n est définie par le vecteur Pⁿ de composantes:

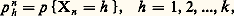tel que Pⁿ = MⁿP ⁰.

La matrice carrée d’ordre k des probabilités de passage entre t et t + n est indépendante de t et vaut:

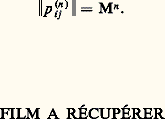Le problème le plus important concerne le comportement limite, pour n infini, de Mⁿ et de Pⁿ . La solution complète de ce problème est obtenue par l’analyse spectrale de l’opérateur linéaire M (cf. théorie SPECTRALE et calcul des PROBABILITÉS, chap. 10); mais des renseignements très importants sont obtenus par l’étude algébrique directe qui consiste à établir une relation de préordre sur les états: l’état j est dit conséquent de l’état i s’il existe n 礪 0 tel que p^nij 礪 0. On note ij . Après réduction par la relation d’équivalence 轢練練良, on obtient une relation d’ordre sur les classes d’états (deux états de la même classe sont mutuellement conséquents l’un de l’autre).

La classe II est dite conséquente de la classe I, car tout état de II est conséquent de tout état de I. Les classes I et II sont dites classes de passage , tandis que les classes III et IV sont dites classes finales . Les états qui les composent sont dits états finals :

Le système aboutit à une classe finale de laquelle il ne sort plus. À chaque classe finale F^a est associée une valeur propre et une seule de valeur 1; le vecteur propre correspondant P^a a des composantes positives sur tous les états de cette classe, nulles en dehors. Si le système aboutit à la classe F^a , la loi limite des états pour n = 秊 est P^a ; cette loi limite est stable en ce sens que Pⁿ = P^{n +1} = P ^a. Dans ces conditions, la loi des états à la date t est indépendante de t : on dit que le système est en régime stationnaire . Si 劉 ne contient qu’une seule classe finale, alors P size=1^秊 = P ^a, quelle que soit la loi initiale P ⁰; le système est alors dit ergodique .

Cas dénombrable (états récurrents ou non récurrents)

Soit k^nij la probabilité conditionnelle pour qu’on ait E^{t +n} = E^j et E^{t +h} E^j , avec 0 麗 h 麗 n , sachant que E^t = Eⁱ (c’est la probabilité d’un premier passage en E^j à la date t + n à partir de l’état Eⁱ en t ), et soit

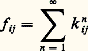la probabilité d’un passage au moins en E^j à partir de l’état Eⁱ .

Un état Eⁱ est dit récurrent si fⁱⁱ = 1; il est dit non récurrent dans le cas contraire. On démontre que tous les états d’une même classe ont le même caractère. Les états d’une classe de passage sont toujours non récurrents; ceux d’une classe finale peuvent être récurrents ou non récurrents (dans le cas fini ils sont toujours récurrents).

Processus de renouvellement

Soit X^t un processus et 劉 un ensemble d’états. On dit que X^t est de renouvellement s’il existe une suite croissante d’instants aléatoires t ¹, t ², ..., tⁿ telle que la connaissance de l’état en tⁿ résume l’information passée utile pour la prédiction. L’exemple le plus simple est le processus ponctuel à intervalles aléatoires indépendants et parents; les instants tⁿ du processus ponctuel sont dits instants (ou points) de renouvellement .

5. Processus laplaciens

On appelle un ensemble de variables aléatoiresX¹, X², ..., Xⁿ ensemble laplacien si, et seulement si, toute forme linéaire de ces variables, c’est-à-dire toute variable aléatoire Z = aⁱ Xⁱ , obéit à une loi de Laplace-Gauss ^{[cf. PROBABILITÉS (CALCUL DES)]}. Dans ces conditions, chaque variable aléatoire Xⁱ obéit à une loi de Laplace-Gauss; soit mⁱ = E(Xⁱ ) sa valeur moyenne.

La loi jointe de l’ensembleXⁱ est de la forme:

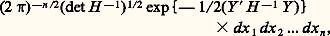où Y est le vecteur colonne de composantes(xⁱ 漣 mⁱ ) et Y le transposé; H est la matrice n 憐 n des variances et covariances:

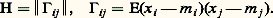La loi de l’ensemble est donc complètement définie par la donnée des moments du premier et du second ordre de l’ensemble des variables.

On dit qu’un processus X^t est un processus laplacien si pour tout k , quels que soient t ¹, t ², ..., t^k , l’ensemble aléatoire correspondantX¹, X², ..., X^k est un ensemble laplacien.

La loi temporelle du processus est définie par deux fonctions certaines du temps, la valeur moyenne:

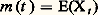et la fonction de covariance:

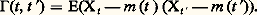Toute forme linéaire à coefficients constants de X^t est une variable aléatoire laplacienne (ou normale). L’ensemble de ces formes est un espace vectoriel qu’on peut munir d’un produit intérieur (espérance du produit): on obtient alors un espace préhilbertien. On peut l’orthogonaliser selon le procédé de Schmidt (cf. théorie SPECTRALE); des variables laplaciennes orthogonales sont indépendantes. On peut aussi représenter tout ensemble de valeurs Y¹, Y², ... à partir de variables indépendantes laplaciennes U¹, U², ... selon un développement du type suivant, dit développement canonique de Paul Lévy.

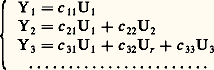Processus stationnaires

Si, quels que soient t et t , le nombre 臨(t + h , t + h ) est indépendant de h , on dit que le processus est stationnaire ; la fonction de covariance ne dépend plus alors que d’une seule variable h = t 漣 t . On pose:

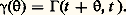Toute fonction 塚( ) ainsi obtenue est de type non négatif , et S. Bochner a montré, en 1932, que, si 塚( ) est continue à l’origine, elle est continue partout, et il existe une fonction à valeurs réelles A( 諸) monotone croissante et à variation bornée telle que:

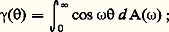la fonction A( 諸) est dite fonction de distribution spectrale du processus X^t .

Tout processus laplacien stationnaire centré X^t peut être obtenu par superposition (ou somme) de processus du type suivant:

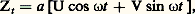où a et 諸 sont des constantes réelles et U et V des variables de Laplace-Gauss centrées réduites indépendantes. Un tel processus Z^t est un processus laplacien stationnaire; sa fonction de covariance est a ² cos 諸.

Processus stationnaire du second ordre et analyse harmonique

Soit Z^t un processus à valeurs complexes, soit E(Z^t ) = m (t ) et posons X^t = Z^t 漣 m (t ). Le processus est dit stationnaire du second ordre si m (t ) et E(X^{t +} size=1X^t ) sont des fonctions définies indépendantes de t ; la fonction:

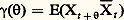est dite fonction de covariance . On suppose, enfin, que la partie réelle de 塚( ) est continue à l’origine, ce qui équivaut à supposer que X^t est continue en moyenne quadratique. Les premiers travaux sur cette classe importante de processus sont dus à N. Wiener (1930). A. Khintchine (1934), R. Fortet et A. Blanc-Lapierre (1953). Les fonctions 塚( ) introduites ici sont, à un multiplicateur positif près, des fonctions caractéristiques. Ainsi à toute fonction 塚( ) est associée une fonction A( 諸) à valeurs réelles, monotone croissante et à variation bornée telle que:

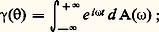la fonction A( 諸) est dite fonction de distribution spectrale .

Composition de processus orthogonaux par superposition

Soit U^t et V^t deux processus centrés du second ordre. Ils sont dits orthogonaux si, quels que soient t et t , on a E(U^t V^t size=1) = 0; soit g ¹( ) et g ²( ) les fonctions de covariances de ces processus. Formons:

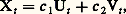où c ¹ et c ² sont des constantes complexes. Alors X^t est un processus centré du second ordre, et sa fonction de covariance est:

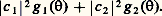En particulier Z^t = U e ^it size=1^諸, équation où U est une variable aléatoire centrée réalisant E(|U|²) = 1, est un processus stationnaire de fonction de covariance e ⁱ size=1^諸. Le processus X^t qui admet 塚( ) pour fonction de covariance peut être obtenu par composition de processus orthogonaux, ce qui a permis à Paul Lévy d’adopter la notation, qui traduit la construction effectuée,

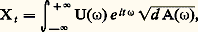où les U( 諸) sont des variables aléatoires orthogonales. Ainsi, la théorie des processus laplaciens est la même que celle des processus du second ordre; mais, dans ce dernier cas, on ne s’intéresse qu’aux moments du premier et du second ordre des variables considérées.

Encyclopédie Universelle. 2012.